From the Narrow Desert: Geometry

Showing posts with label Geometry. Show all posts

Wednesday, December 7, 2022

More weird student telepathy/coincidences

The solfeggio scale has been in the sync stream recently, and I have written a few posts about it. Today one of my young students ran up to the stairs to the classroom, shouting, "Do re me fa sol la ti do!" as he did so. (I suppose this highlights one of the metaphorical meanings of the scale: step-by-step ascent. Likewise, the descending scale which begins "Joy to the World" is an appropriate symbol of the descent of the Lord to earth.)

When I myself entered the classroom, I found someone had doodled this on the board:

This was just a quick freehand sketch, obviously, but it demonstrates some of the geometric properties of the pentagram (five-pointed star), and of stars whose points touch the points of other stars.

Sometimes, as a way of focusing my mind, I like to do some traditional geometric construction work with a compass and straightedge. Just this morning, I had done this:

After finishing this, I noticed that, as a by-product of the process of constructing the pentacle, I had drawn a circle below it, with four of the six vertices of a hexagon already marked. I intended to use these to construct a hexagram (six-pointed star), two of the tips of which would touch two of the tips of the pentagram. Unfortunately, I had to go to work and didn't have time to finish this last step. Then later in the day I found an extremely similar geometric concept illustrated on my whiteboard!

Update: This is what I had intended to draw, and did finish drawing after the class.

Update 2: In the 1990s, the Church of Jesus Christ of Latter-day Saints changed their logo so that the name "JESUS CHRIST" was much, much larger than everything else -- presumably under the misapprehension that this would put an end to the whole "Mormons aren't Christians" thing. Yesterday, after posting this, I wanted to look up when exactly this happened, and in the course of researching the history of the Mormon logo, I ended up perusing a post by architect Brandon Ro called "Sacred Geometry in new Church Symbol." Mr. Ro writes:

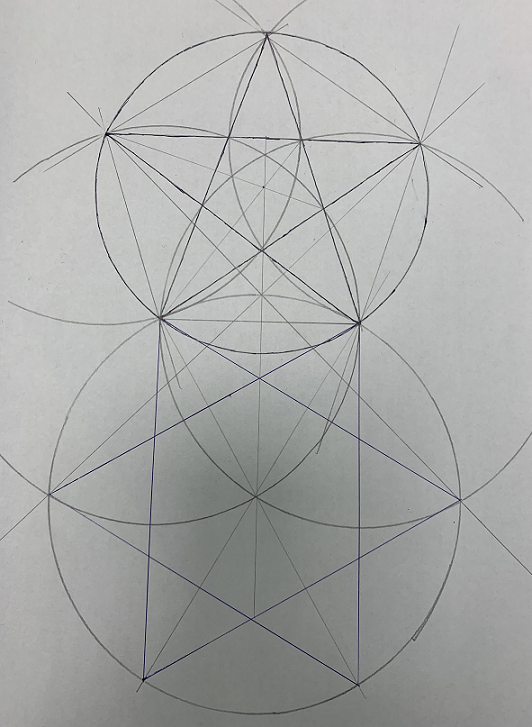
About six years ago I had a memorable lunch conversation with a couple of friends who were in the process of working on a new symbol/logo for The Church of Jesus Christ of Latter-day Saints. They told me that the symbol needed to emphasize the importance and centrality of Jesus Christ within the Church. It also needed to speak a universal language applicable to people around the world through iconography and symbolism. From a cross, star of David (6-pointed star), squared circle, pentagram (5-pointed star), and seal of Melchizedek (8-pointed star) just about everything was considered. I provided them with a few resources on sacred geometry and symbols.

Besides being another synchronicity, isn't that just weird? How could they possibly have considered the star of David (universally recognized as a symbol of Judaism) or the pentagram (associated in the popular mind with Satanism) as potential symbols of Mormonism? (The symbol they finally ended up with looks an awful lot like the Catholic "Mary on the Half Shell.")

Of course I have to comment on the eight-pointed star, too. (Hi, Debbie!) I'm not exactly a stranger to sacred geometry, but this was the first I'd ever heard of the "seal of Melchizedek." It turns out this is a fairly recent bit of Mormon folklore, derived from a illustrator's caption in one of Hugh Nibley's books. Pre-Nibley, there's no tradition of associating the eight-pointed star with Melchizedek (A separate bit of Mormon folklore postulates that Melchizedek was the same person as Shem, son of Noah, one of the "eight souls saved by water," so there's that.)

It's a striking symbol, and an easy one to draw in MSPaint, but I think the Church was right not to go with it. It looks either Islamic or New-Agey and would reinforce the unwanted association between Mormonism and such "cults" as Scientology and Raelism.

Monday, June 21, 2021

Using daylight phases of the Moon to calculate the relative distance of the Sun and the Moon

As everyone knows, the Moon is sometimes visible during the day, while the Sun is also in the sky. Suppose you look up sometime during the day and see a half-moon in the sky. The Sun is also in the sky, separated from the Moon by 45 degrees of arc. What can you conclude from this?

In the above diagram, the vertical ray (using that word in the geometric, not the optical, sense) represents all possible locations of the Moon. (Since we are supposing we do not know how far the Moon is from the Earth, it could in principle be at any point along the ray.) The diagonal ray represents all possible locations of the Sun when it appears from Earth to be 45 degrees distant from the Moon. The horizontal ray extending out from the Moon represents all possible locations of the Sun which would cause a half-moon to be visible from Earth. Therefore, if you see a half-moon 45 degrees from the Sun, you can conclude that the Sun is 1.414 (the square root of two) times as far from the Earth as the Moon is -- and that therefore everything you know about astronomy is wrong, since astronomers tells us the Sun is approximately 395.5 times as far from Earth as the Moon is.

If that figure is correct, what should be the angular distance between the Sun and a half-moon? Well, it must be less than 90 degrees, since the red ray (representing the Sun at 90 degrees from the Moon) is parallel to, and thus never intersects, the half-moon ray. But, since 395.5 is a very large number, it must be only a little less than 90 degrees. I've forgotten all my trigonometry, so I'll leave the exact figure as an exercise for the reader.

Update: I've just realized the flaw in this reasoning -- that it applies only when the Moon is directly overhead. The angular elevation of the Moon must be included in the equation, not only its angular distance from the Sun.

Update 2: No, on second thought, I think I was right the first time.

Sunday, November 24, 2019

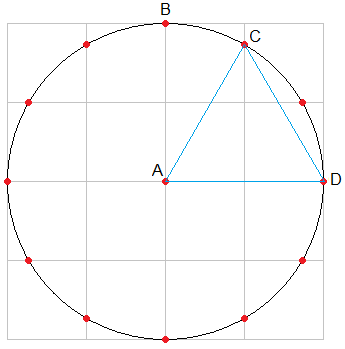
Proof that a 4-by-4 grid divides a circle into 30-degree arcs

This turned out to be almost disappointingly easy to prove.

AC is equal in length to AD, since they are radii of the same circle. C is on the vertical line that bisects AD. Therefore, CD is the mirror image of AC, and the triangle ACD is equilateral. Therefore, the angle formed by AC and AD is 60 degrees, and that formed by AB and AC is 30 degrees.

Similar triangles can be made for all the other red points, showing that they are located at 30-degree intervals.

No other grids (3-by-3, 5-by-5, etc.) divide a circle evenly like this.

Another mathematical puzzle: Why does this work?

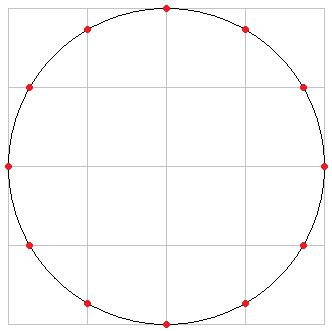
Never having bothered to acquire any halfway decent graphics software, I've been using this trick for years to draw regular hexagons, equilateral triangles, and such.

Create a 4-by-4 grid of squares and inscribe a circle in it. The lines of the squares will intersect the circle at 12 points, which appear to be equally spaced at 30-degree intervals around the circumference of the circle. You can then connect selected points to create a triangle, hexagon, or dodecagon.

(The ancient geometers used to take it as a challenge to construct various polygons using only a square and compass. I suppose the modern equivalent would be: Using only a crappy graphics program like MS Paint, construct . . . .)

I can't remember how I happened to discover this -- just one of those happy accidents, I think. I also can't be sure, absent any mathematical proof, that the points are really evenly spaced at 30-degree intervals. (If not, they are certainly close enough that the trick can still be used to create polygons that seem to the human eye to be perfectly regular.) However, I strongly suspect that they are perfectly regularly spaced, because that's just how math is.

The last mathematical proof I embarked on, regarding congruence patterns in triangular numbers (qv) was a matter of straightforward number theory, requiring only everyday algebra, which is why I was never really in any doubt as to my ability to solve it. I am much less confident of my competence in this case, though, being innocent even of basic trigonometry. (Obviously somebody invented trigonometry without having been taught it, and I'm sure I could do the same if push came to shove; the question is whether or not I want to invest so much time and thought in a problem which has elicited only my passing curiosity.)