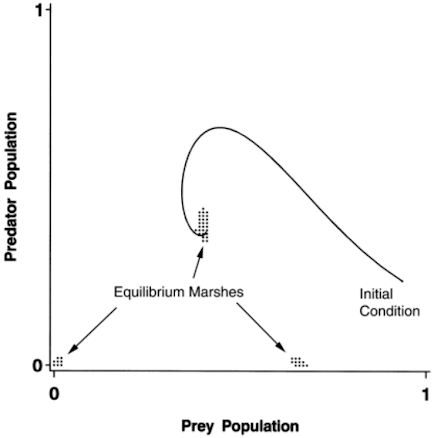
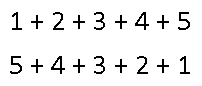Especially with social science topics in which change is slow, differential equation systems often do not have a chance to evolve to the point where the system trajectories actually arrive at an equilibrium. In reality, the trajectories "bog down" when they pass anywhere near the equilibrium in what is called an "equilibrium marsh." Placing the equilibrium marshes in the phase diagram is a useful way to identify those areas where trajectory velocity is so slow that the system essentially comes to a near halt even though equilibrium has not been achieved (p. 56).
Tam multa, ut puta genera linguarum sunt in hoc mundo: et nihil sine voce est.
Friday, March 22, 2024
Equilibrium marshes
Tuesday, March 28, 2023
Are the Irish better at math?
Studies have shown that Irish people are significantly better than non-Irish at solving this math problem. Remarkably, many of them are able to do so in a matter of seconds, without using a calculator or even a pencil and paper. The problem is as follows:
Suppose there is a population of hares which, though every bit as prolific as lagomorphs generally are, are heavily hunted and thus increase in numbers very, very slowly. In fact, from one year to the next, the hare population only increases by an average of 0.005615%. To the casual observer, the hares' numbers appear to be static, but in fact the population is slowly but surely growing and, given enough time, will eventually double. It's a long road, but in the end they will arrive there. Assuming the rate of increase does not change, precisely how many years will it take the hare population to traverse this rocky road to doubling?
 |
| Hannah Gifford, Hare and the Blackthorn Blossom |
Monday, January 30, 2023
Lewis Carroll syncs
Today I was watching a math video (as one does) by Michael Penn that was his solution to a problem posed by Lewis Carroll (C. L. Dodgson) in the 1893 work Curiosa Mathematica II or Pillow Problems. Online I found a .djvu file of a reprint published in 1958 as The Mathematical Recreations of Lewis Carroll, which contains 72 problems Dodgson originally worked out in his head.Problem 58 was originally worked out by Dodgson on the 20th of January 1884 and its text reads as follows:"Three Points are taken at random on an infinite Plane. Find the chance of their being the vertices of an obtuse-angled Triangle."Dodgson provides his solution in which he constructs a shape composed of two arcs and a line segment. Rescaling the triangle and equating its longest side to the line segment, all possible triangles (scaled appropriately) are contained within the shape. He also includes a semicircle with the diameter being the line segment.Michael Penn follows the same basic approach in that he constructs the same shapes, but he includes their reflections across the line segment. This, of course, results in a drawing of a vesica containing a circle, a shape that has been in the syncs.I also note that the infinite plane the three points are selected from is a "flat plane" as discussed above.
I was just reading a question and answers on Stack Overflow for something at work, and I happened to notice one of the Hot Network Questions in the right sidebar was "In honor of Lewis Carroll’s birthday, January 27."When I submitted the above comment in both of our time zones it was January 27. I did not know that that is the birthday of Lewis Carroll until just now.
I didn't know that yesterday was Lewis Carroll's birthday, either. I read this passage in Green Doors yesterday. Petra, private secretary to a psychiatrist, is snooping in the doctor's files, looking for the records on a patient named McCloud.
Petra was pulling out the drawer marked in small black letters Mc. She pulled it slowly, as one might open a door onto an unknown landscape. She herself thought of Alice. "It might be the rabbit hole and here I am on the verge of tumbling down it." Indeed, she felt herself a second Alice and as if this deep drawer held a wonderland into which she was about to escape from the stifling hot afternoon of the upper world. Could she had known what it held for her, how different her hesitation in going on pulling out the drawer would have been, how much faster her heart would have beat!
Just saw on TV an ad for the show "Pawn Stars.""Alice in Wonderland," said a voice and then, immediately, the scene changing, "Tyrannosaurus teeth are really rare."
Lewis Carroll, as a Victorian writer known for "nonsense," has much in common with his older contemporary Edward Lear.
Saturday, January 14, 2023
A little 1/14 coincidence
And in the fourteenth day of the first month is the passover of the Lord.
And they departed from Rameses in the first month, on the fifteenth day of the first month; on the morrow after the passover the children of Israel went out with an high hand in the sight of all the Egyptians.
Thursday, March 3, 2022
No two points on an infinite line are infinitely distant
I mentioned this in passing in "What if there was no beginning?" in connection with the Kalām Paradox. but I think it deserves a post of its own.
The Kalām Paradox, for those who came in late, asserts that nothing temporal can have always existed. If it had, it would be infinitely old, meaning that an infinite amount of time must already have elapsed. However, it is impossible for an infinite amount of time to elapse, because time elapses one finite step at a time, and adding up finite quantities can never yield an infinite quantity.
⁂
First, I should make it explicit what sort of infinity we're talking about here. We're not talking about Zeno's paradoxes which find an uncountable infinity within countably finite quantities. In the racecourse paradox, for example, it is supposed to be impossible to run a mile, because first you have to run half a mile; and before you can run half a mile, you have to run a quarter of a mile; and so on -- an infinite number of tasks. A number-theoretical way of expressing this is that between any two integers there are (uncountably) infinitely many real numbers. To apply Zeno's spatial paradox to time, we could say it is impossible for anyone or anything to be a year old -- because before a year can elapse, 6 months have to elapse; before 6 months, 3 months; and so on -- a sum of infinitely many finite quantities, which must therefore add up to infinity. This is not the Kalām argument, which takes it for granted that things can have a finite age.
I will not bother to address Zeno-type paradoxes because no one is in any danger of believing them. The Johnsonian "I refute it thus!" is sufficient. It's very obvious that fleet-footed warriors can catch tortoises, and that it is in fact possible to run a mile. These are matters of everyday observation, as the subject matter of Kalām -- the question of whether the universe had a beginning -- cannot be.
⁂
When the Kalām Paradox denies that the past can be infinite, it is referring to countable infinity, of which the paradigm case is not the real numbers but the integers. (To be sure, time may also be infinitely divisible and thus uncountably infinite, but that is a separate question.) The image we want to keep in mind, then, is the integer number line.
Monday, June 21, 2021
Using daylight phases of the Moon to calculate the relative distance of the Sun and the Moon
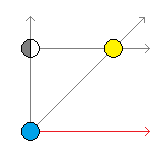
As everyone knows, the Moon is sometimes visible during the day, while the Sun is also in the sky. Suppose you look up sometime during the day and see a half-moon in the sky. The Sun is also in the sky, separated from the Moon by 45 degrees of arc. What can you conclude from this?
In the above diagram, the vertical ray (using that word in the geometric, not the optical, sense) represents all possible locations of the Moon. (Since we are supposing we do not know how far the Moon is from the Earth, it could in principle be at any point along the ray.) The diagonal ray represents all possible locations of the Sun when it appears from Earth to be 45 degrees distant from the Moon. The horizontal ray extending out from the Moon represents all possible locations of the Sun which would cause a half-moon to be visible from Earth. Therefore, if you see a half-moon 45 degrees from the Sun, you can conclude that the Sun is 1.414 (the square root of two) times as far from the Earth as the Moon is -- and that therefore everything you know about astronomy is wrong, since astronomers tells us the Sun is approximately 395.5 times as far from Earth as the Moon is.
If that figure is correct, what should be the angular distance between the Sun and a half-moon? Well, it must be less than 90 degrees, since the red ray (representing the Sun at 90 degrees from the Moon) is parallel to, and thus never intersects, the half-moon ray. But, since 395.5 is a very large number, it must be only a little less than 90 degrees. I've forgotten all my trigonometry, so I'll leave the exact figure as an exercise for the reader.
Update: I've just realized the flaw in this reasoning -- that it applies only when the Moon is directly overhead. The angular elevation of the Moon must be included in the equation, not only its angular distance from the Sun.
Update 2: No, on second thought, I think I was right the first time.
Friday, March 26, 2021
Calculating beta diversity
Diversity? Comme au courant! Well, you know I like to cover all the bases.
⁂
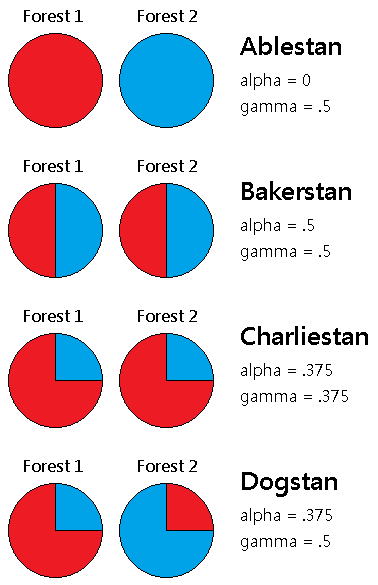
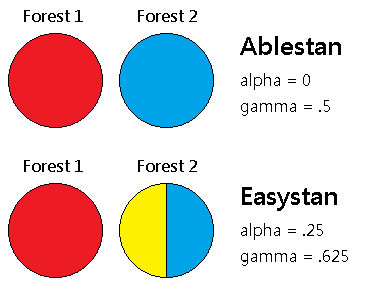
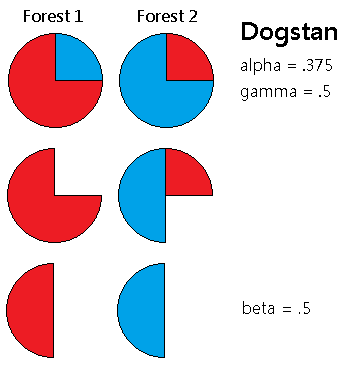
There are (or were when I was in college) three types of ecological diversity: alpha, beta, and gamma. Let's say we're talking about a territory in which there are a number of separate forests, each of which contains a number of trees which may be classified into discrete species.
Gamma diversity is the total diversity of trees within the territory. If we select two of the territory's trees at random, what is the probability that they will be of different species? That number (a "diversity index") would be a quantification of the territory's gamma diversity. You can think of the gamma as standing for global; we're looking at the diversity of individuals (trees) in the entire territory, without considering any of the smaller subgroups (forests) among which those individuals are distributed.
Alpha diversity is the diversity of trees within each forest. If we randomly select two trees from the same forest, what is the probability that they will be of different species? This is an index of alpha diversity. Think of alpha as representing the article a -- the internal diversity within a single forest. We can calculate a diversity index for each of the forests in the territory, and the mean of these numbers will be the alpha diversity of the territory as a whole.
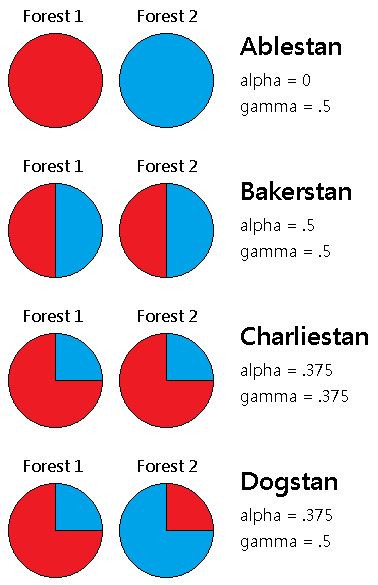
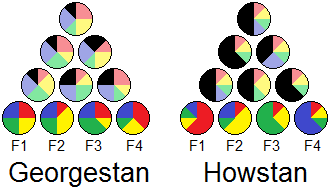
For maximum simplicity, let's just look at territories that have only two forests (Forest 1 and Forest 2), which each have the same number of trees, and only two tree species (redwoods and bluewoods).
- Georgestan
- gamma = 75%
- alpha = 72.7%
- beta = 18.8%
- Howstan
- gamma = 75%
- alpha = 57.8%
- beta = 52.1%
- Itemstan
- gamma = 75%
- alpha = 75%
- beta = 0%
- Jigstan
- gamma = 75%
- alpha = 0%
- beta = 100%
Saturday, December 26, 2020
The distribution of mixed polyhedral dice rolls
In a recent post, Kevin McCall wrote,
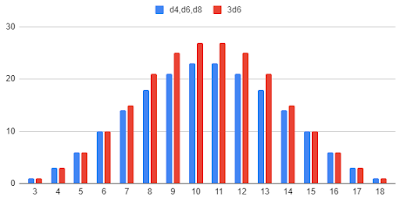
We might compare [a particular hypothetical distribution of IQs] to rolling all 5 Platonic solids: one 4 sided die, one 6 sided, one 8 sided, one 12 sided, and one 20 sided, which would have a completely different distribution from rolling five 6-sided dice.
And I commented,
Would rolling a mix of polyhedral dice really result in anything significantly different from a normal bell curve. I haven’t done the calculations, but my assumption is that it would not.
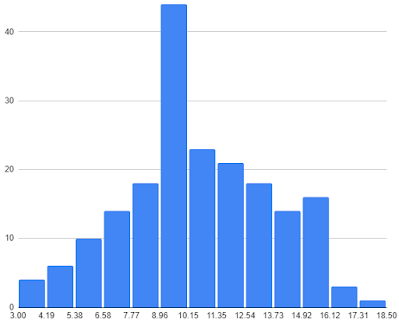
Then I almost immediately retracted this statement ("Never mind. I've checked it, and my assumption was totally wrong!") because I'd put the possible rolls of three dissimilar dice (a d4, a d6, and a d8) into a spreadsheet and it had given me a histogram that looked nothing like a normal distribution.
But now I have to retract that retraction and reaffirm my original assumption. The weird-looking histogram is an artifact. Rolling the three dice mentioned yields one of 16 possible values, from 3 to 18, but the spreadsheet software (Google Sheets) for some reason made a histogram with only 13 bars. Most of the bars represent a single value, but 3-4, 9-10, and 15-16 are grouped together, which is why those three bars are abnormally tall. Making a 16-bar histogram by hand, I find that rolling mixed dice does after all yield a normal bell curve.
The moral of the story: If it comes down to trusting either your own instincts or the basic competence of Google programmers, go with your own instincts every time!
But you already knew that.
Monday, March 2, 2020
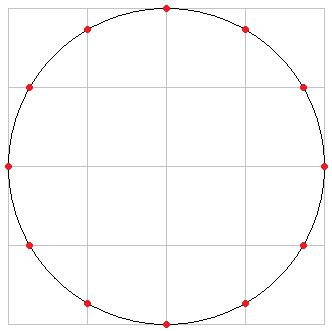
Visualizing gnomon series for the figurate numbers modulo 10
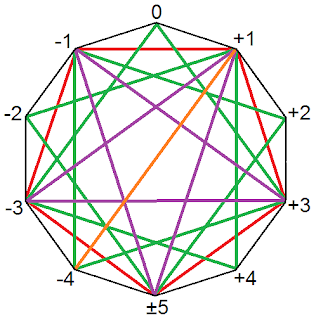
The number that may be added to the nth figurate number to yield the (n + 1)th is called a gnomon. To generate the series of triangular numbers, you start with 0, then add 1, then add 2, then add 3, and so on through the natural numbers. In other words, the gnomon series for triangular numbers is (1, 2, 3, 4, 5, 6, 7, ...) -- which is congruent (mod 10) to (+1, +2, +3, +4, ±5, -4, -3, -2, -1, 0) endlessly repeated. To get the gnomon series for the triangular numbers, start at +1 on the decagon and follow the black lines clockwise.
For the triangular numbers, the difference between the nth gnomon is the (n - 1)th gnomon is 1. I shall express this by saying that the gnomon interval for the triangular numbers is 1. For the squares, the gnomon interval is 2; for the pentagonal numbers, it is 3; and so on. The gnomon interval for the n-gonal numbers is always equal to n - 2.
The gnomon series for the n-gonal numbers modulo 10 may be read off our decagon by starting at +1 and going clockwise, reading every (n - 2)th vertex. It is readily apparent that there are only 10 possible gnomon series, since reading every (n + 10)th vertex is the same as reading every nth vertex. The gnomon series are:
- 3-gonal: black lines clockwise (+1, +2, +3, +4, ±5, -4, -3, -2, -1, 0)
- 4-gonal: red lines clockwise (+1, +3, ±5, -3, -1)
- 5-gonal: green lines clockwise (+1, +4, -3, 0, +3, -4, -1, +2, ±5, -2)
- 6-gonal: purple lines clockwise (+1, ±5, -1, +3, -3)
- 7-gonal: orange line (+1, -4)
- 8-gonal: purple lines counterclockwise (+1, -3, +3, -1, ±5)
- 9-gonal: green lines counterclockwise (+1, -2, ±5, +2, -1, -4, +3, 0, -3, +4, +1)
- 10-gonal: red lines couterclockwise (+1, -1, -3, ±5, +3)
- 11-gonal: black lines counterclockwise (+1, 0, -1, -2, -3, -4, ±5, +4, +3, +2)
- 12-gonal: only one vertex (+1)
Two tasks remain: (1) proving what I have just asserted, and (2) devising a way to predict, for any modulus, which gnomon intervals will yield a left-right symmetrical pattern.
Monday, February 17, 2020
Applying Kevin McCall's logic to squares and other non-centered figurate numbers
The series of triangular numbers is generated by starting with 0, then adding 1, then adding 2, then 3, and so on through the succession of natural numbers. Due to the fact that k - n ≡ -n (mod k), one you've added numbers up to a certain point, you start doing the modular equivalent of subtracting those same numbers in reverse order, creating a palindrome.Thus, if we consider the sequence of triangular numbers reduced modulo 10:
- 0
- +1
- +2
- +3
- +4
- +5
- +6 ≡ -4 (mod 10)
- +7 ≡ -3 (mod 10)
- +8 ≡ -2 (mod 10)
- +9 ≡ -1 (mod 10)
- +10 ≡ 0 (mod 10)
- +11 ≡ +1 (mod 10)
- +12 ≡ +2 (mod 10)
- +13 ≡ +3 (mod 10)
- +14 ≡ +4 (mod 10)
- +15 ≡ -5 (mod 10)
- +16 ≡ -4 (mod 10)
- +17 ≡ -3 (mod 10)
- +18 ≡ -2 (mod 10)
- +19 ≡ -1 (mod 10)
- +20 ≡ +0 (mod 10)
- etc.
At the end of this 20-step cycle, we are back where we started, with a number that is congruent to 0 (mod 10), and the cycle starts again.
Note that we have to go through two cycles of adding and subtracting the numbers because +5 ≡ -5 (mod 10). We count it as +5 the first time around and -5 the second time, so that it cancels out. If the modulus is odd, only one cycle is necessary.
- 0
- +1
- +3
- +5
- +7 ≡ -3 (mod 10)
- +9 ≡ -1 (mod 10)
- +11 ≡ +1 (mod 10)
- +13 ≡ +3 (mod 10)
- +15 ≡ -5 (mod 10)
- +17 ≡ -3 (mod 10)
- +19 ≡ -1 (mod 10)
- etc.
- 0
- +1
- +4
- +7
- +10 ≡ +0 (mod 10)
- +13 ≡ -7 (mod 10)
- +16 ≡ -4 (mod 10)
- +19 ≡ -1 (mod 10)
- +22 ≡ +2 (mod 10)
- +25 ≡ +5 (mod 10)
- +28 ≡ +8 (mod 10)
- +31 ≡ +1 (mod 10)
- +34 ≡ +4 (mod 10)
- +37 ≡ +7 (mod 10)
- +40 ≡ +0 (mod 10)
- +43 ≡ -7 (mod 10)
- +46 ≡ -4 (mod 10)
- +49 ≡ -1 (mod 10)
- +52 ≡ -8 (mod 10)
- +55 ≡ -5 (mod 10)
- +58 ≡ -2 (mod 10)
- +61 ≡ +1 (mod 10)
- etc.
- 0
- +1
- +6
- +11 ≡ +1 (mod 10)
- +16 ≡ +6 (mod 10)
- +21 ≡ +1 (mod 10)
- +26 ≡ +6 (mod 10)
- +31 ≡ +1 (mod 10)
- +36 ≡ +6 (mod 10)
- etc.
Sunday, February 16, 2020
Are all reduced sequences of figurate numbers repeating palindromes?
Preliminaries: Terminology and notation
A palindrome is any series of elements that is the same forwards and backwards. Each palindrome thus consists of two parts, which we shall call the head and the tail. The tail consists of the same series of elements as the head, but in reverse order. For example, in the palindromic word “noon,” the string “no” is the head, and “on” is the tail. In “noon,” the head and tail are entirely separate, but in a palindrome with an odd number of elements, the end of the head will overlap with the beginning of the tail. For example, the head of the palindromic word “level” is “lev,” and the tail is “vel”; a single “v” does double duty as the last element of the head and the first element of the tail.
No special notation is required to write a simple palindrome such as “noon” or “level,” but we are concerned in this post with repeating palindromic series (RPSs). If a palindrome consists of a head followed by a tail (possibly overlapping), an RPS is a head followed by a tail, then the head again, then the tail again, and so on to infinity. In the notation we will be using here, an RPS is represented by "RPS" followed by its head enclosed in parens (round brackets), thus:
- RPS (no) = noonnoonnoonnoonnoon...
If the end of the head overlaps with the beginning of the tail, an additional open-paren is placed before the first element of the tail, thus:
- RPS (le(v) = levellevellevellevellevel...
In an RPS, unlike a simple palindrome, overlap at the other end is also possible. For example, the word “grammar” is not itself a palindrome, but “grammar” endlessly repeated is an RPS. The letter “g” is both the beginning of the head and the end of the tail. This sort of overlap is indicated by placing a close-paren after the last element of the tail, thus:
- RPS (g)ram) = grammargrammargrammar...
It is possible to have overlap at both ends, as in this example.
- RPS (v)oo(d) = voodoovoodoovoodoo...
Overlap need not be limited to a single element; it can be a series of elements, provided that series is itself a palindrome. For example, consider the RPS created by endlessly repeating the word “sestet.”
- RPS (ses)t(e) = sestetsestetsestetsestet...
I should also mention that, much like a repeating decimal, an RPS has a beginning but not an end. As with a decimal like 0.16666666..., there may be a non-repeating segment at the beginning, before the RPS proper starts. Our notation can deal with this by putting this non-repeating segment before the first paren, as in this example.
- RPS n(eve)(r) = neverevereverevereverever...
One final note about the notation: If each element in the RPS can be represented by a single character (a letter, a one-digit number, etc.), it can be written as in the examples above, without commas or spaces. If the elements of an RPS are words, multidigit numbers, etc., the elements should be separated by commas and spaces.
Several posts on this blog have dealt with the fact that, for any modulus k, the sequence of triangular numbers reduced modulo k will be an RPS. Two different proofs of this have been given (here and here). The pattern is easiest to see when k = 10, since (in the decimal system) any number reduced modulo 10 is equal to the final digit of that number.
The first several triangular numbers are: 0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666...
If we reduce that sequence modulo 10 (by replacing each number in the sequence with its final digit), we get: 0, 1, 3, 6, 0, 5, 1, 8, 6, 5, 5, 6, 8, 1, 5, 0, 6, 3, 1, 0, 0, 1, 3, 6, 0, 5, 1, 8, 6, 5, 5, 6, 8, 1, 5, 0, 6...
This reduced sequence is RPS (0136051865). Any other modulus will also yield an RPS.
Square numbers
Only some three months after proving the RPS theorem for triangular numbers did I notice that the sequence of square numbers shows a similar pattern. Below are the square numbers from 02 to 502. Start at the upper left, follow the zigzag down to the bottom, and then come back up the zigzag on the right.
Numbers in the same column have the same last digit (i.e., are congruent modulo 10). Numbers in the same row have the same last two digits (i.e., are congruent modulo 100).
Square numbers reduced modulo 10 = RPS (0)1496(5).
Square numbers reduced modulo 100 = RPS (0), 1, 4, 9, 16, 25, 36, 49, 64, 81, 0, 21, 44, 69, 96, 25, 56, 89, 24, 61, 0, 41, 84, 29, 76, (25).
I haven't checked if other moduli also yield RPSs, but, based on my experience with triangular numbers, and on the general principle that there is nothing mathematically special about powers of 10, I feel quite certain that they do.
Octagonal numbers reduced modulo 10 = RPS (01810)56(3)
Enneagonal numbers reduced modulo 10 = RPS (0194651441564910)69)
Decagonal numbers: 0, 1, 10, 27, 52, 85, 126, 175, 232, 297, 370, 451, 540, 637, 742, 855, 976, 1105, 1242, 1387, 1540, 1701, 1870, 2047, 2232, 2425, 2626, 2835, 3052, 3277, 3510, 3751, 4000, 4257, 4522, 4795, 5076, 5365, 5662, 5967, 6280, 6601, 6930, 7267, 7612, 7965, 8326
Decagonal numbers reduced modulo 10 = RPS (010)725(6)
Centered figurate numbers
Centered triangular numbers: 1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199, 235, 274, 316, 361, 409, 460, 514, 571, 631, 694, 760, 829, 901, 976, 1054, 1135, 1219, 1306, 1396, 1489, 1585, 1684, 1786, 1891, 1999, 2110, 2224, 2341, 2461, 2584, 2710, 2839, 2971, 3106, 3244, 3385, 3529
Centered triangular numbers reduced modulo 10 = RPS (1409164596)
Centered square numbers: 1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265, 313, 365, 421, 481, 545, 613, 685, 761, 841, 925, 1013, 1105, 1201, 1301, 1405, 1513, 1625, 1741, 1861, 1985, 2113, 2245, 2381, 2521, 2665, 2813, 2965, 3121, 3281, 3445, 3613, 3785, 3961, 4141, 4325, 4513
Centered square numbers reduced modulo 10 = RPS (15(3)
Centered pentagonal numbers: 1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, 391, 456, 526, 601, 681, 766, 856, 951, 1051, 1156, 1266, 1381, 1501, 1626, 1756, 1891, 2031, 2176, 2326, 2481, 2641, 2806, 2976, 3151, 3331, 3516, 3706, 3901, 4101, 4306, 4516, 4731, 4951, 5176, 5406
Centered pentagonal numbers reduced modulo 10 = RPS (16)
Hex numbers: 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, 469, 547, 631, 721, 817, 919, 1027, 1141, 1261, 1387, 1519, 1657, 1801, 1951, 2107, 2269, 2437, 2611, 2791, 2977, 3169, 3367, 3571, 3781, 3997, 4219, 4447, 4681, 4921, 5167, 5419, 5677, 5941, 6211, 6487
Hex numbers reduced modulo 10 = RPS (17(9)
Centered heptagonal numbers: 1, 8, 22, 43, 71, 106, 148, 197, 253, 316, 386, 463, 547, 638, 736, 841, 953, 1072, 1198, 1331, 1471, 1618, 1772, 1933, 2101, 2276, 2458, 2647, 2843, 3046, 3256, 3473, 3697, 3928, 4166, 4411, 4663, 4922, 5188, 5461, 5741, 6028, 6322, 6623, 6931, 7246
Centered heptagonal numbers reduced modulo 10 = RPS (1823168736)
Centered octagonal numbers (i.e., odd squares): 1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089, 1225, 1369, 1521, 1681, 1849, 2025, 2209, 2401, 2601, 2809, 3025, 3249, 3481, 3721, 3969, 4225, 4489, 4761, 5041, 5329, 5625, 5929, 6241, 6561, 6889, 7225, 7569
Centered octagonal numbers reduced modulo 10 = RPS (19(5)
Centered enneagonal numbers (i.e., every third triangular number): 1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595, 703, 820, 946, 1081, 1225, 1378, 1540, 1711, 1891, 2080, 2278, 2485, 2701, 2926, 3160, 3403, 3655, 3916, 4186, 4465, 4753, 5050, 5356, 5671, 5995, 6328, 6670, 7021, 7381, 7750, 8128, 8515, 8911, 9316
Centered enneagonal numbers reduced modulo 10 = RPS (1085160356)
Centered decagonal numbers: 1, 11, 31, 61, 101, 151, 211, 281, 361, 451, 551, 661, 781, 911, 1051, 1201, 1361, 1531, 1711, 1901, 2101, 2311, 2531, 2761, 3001, 3251, 3511, 3781, 4061, 4351, 4651, 4961, 5281, 5611, 5951, 6301, 6661, 7031, 7411, 7801, 8201, 8611, 9031, 9461, 9901
Centered decagonal numbers reduced modulo 10 = RPS (1)
Centered decagonal numbers reduced modulo 100 = RPS (1, 11, 31, 61, 1, 51, 11, 81, 61, 51)
Star numbers (i.e., centered dodecagonal numbers): 1, 13, 37, 73, 121, 181, 253, 337, 433, 541, 661, 793, 937, 1093, 1261, 1441, 1633, 1837, 2053, 2281, 2521, 2773, 3037, 3313, 3601, 3901, 4213, 4537, 4873, 5221, 5581, 5953, 6337, 6733, 7141, 7561, 7993, 8437, 8893, 9361, 9841, 10333, 10837
Star numbers reduced modulo 10 = RPS (13(7)
It certainly looks as if all such sequences reduce to RPSs, but the unexpected exception of the (non-centered) heptagonal numbers makes me hesitant to jump to that conclusion.
Wednesday, February 12, 2020
It's natural to repeat things 2^n - 1 times.
 |
| Fifteen! Fifteen no's . . . ha ha ha! |
I try to cover all the bases here.
No.
No no no.
No no no no no no no.
No no no no no no no no no no no no no no no.
No no no no no no no no no no no no no no no no no no no no no no no no no no no no no no no.
I find that I can continue this series more-or-less indefinitely: first 1 "no," then 3, then 7, 15, 31, 63, and so on -- each number in the series being twice the previous number, plus one. For me, these are all natural numbers of times to repeat things. I just naturally stop at 2n - 1, without consciously keeping count. (In fact, I only discovered the pattern by recording myself and then going back and counting the no's.)
Try it yourself (preferably not in a public place!). Is this an idiosyncracy of my own, or have I just discovered Tychonievich's First Law of How Many Times People Repeat Things?
Sunday, November 24, 2019
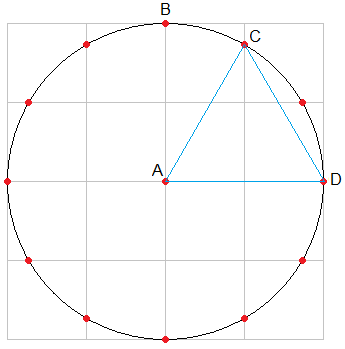
Proof that a 4-by-4 grid divides a circle into 30-degree arcs
AC is equal in length to AD, since they are radii of the same circle. C is on the vertical line that bisects AD. Therefore, CD is the mirror image of AC, and the triangle ACD is equilateral. Therefore, the angle formed by AC and AD is 60 degrees, and that formed by AB and AC is 30 degrees.
Similar triangles can be made for all the other red points, showing that they are located at 30-degree intervals.
No other grids (3-by-3, 5-by-5, etc.) divide a circle evenly like this.
Another mathematical puzzle: Why does this work?
Create a 4-by-4 grid of squares and inscribe a circle in it. The lines of the squares will intersect the circle at 12 points, which appear to be equally spaced at 30-degree intervals around the circumference of the circle. You can then connect selected points to create a triangle, hexagon, or dodecagon.
(The ancient geometers used to take it as a challenge to construct various polygons using only a square and compass. I suppose the modern equivalent would be: Using only a crappy graphics program like MS Paint, construct . . . .)
I can't remember how I happened to discover this -- just one of those happy accidents, I think. I also can't be sure, absent any mathematical proof, that the points are really evenly spaced at 30-degree intervals. (If not, they are certainly close enough that the trick can still be used to create polygons that seem to the human eye to be perfectly regular.) However, I strongly suspect that they are perfectly regularly spaced, because that's just how math is.
The last mathematical proof I embarked on, regarding congruence patterns in triangular numbers (qv) was a matter of straightforward number theory, requiring only everyday algebra, which is why I was never really in any doubt as to my ability to solve it. I am much less confident of my competence in this case, though, being innocent even of basic trigonometry. (Obviously somebody invented trigonometry without having been taught it, and I'm sure I could do the same if push came to shove; the question is whether or not I want to invest so much time and thought in a problem which has elicited only my passing curiosity.)
Tuesday, October 29, 2019
The difference between proof and understanding
Then I read Kevin McCall's much better proofs of the same postulates. What a difference! Where I had hammered out my proofs by algebraic brute force, McCall had understood. -- and left me thinking, in T. H. Huxley's much-quoted words, "How extremely stupid not to have thought of that!"
The heart of McCall's proof is the observation that, in modular arithmetic with modulus k, adding k - n is equivalent to subtracting n. You can easily see this in the most familiar everyday use of modular arithmetic, which is our 12-hour clock, with modulus 12. If you want to get from 11:00 to 7:00, for example, you can either subtract 4 hours or add 12 - 4 = 8 hours.
The series of triangular numbers is generated by starting with 0, then adding 1, then adding 2, then 3, and so on through the succession of natural numbers. Due to the fact that k - n ≡ -n (mod k), one you've added numbers up to a certain point, you start doing the modular equivalent of subtracting those same numbers in reverse order, creating a palindrome. For example, if the modulus is 7:
- 0
- +1
- +2
- +3
- +4 ≡ -3 (mod 7)
- +5 ≡ -2 (mod 7)
- +6 ≡ -1 (mod 7)
- etc.
Why is the period twice as long for even moduli? Consider the case when the modulus is 6.
- 0
- +1
- +2
- +3
- +4 ≡ -2 (mod 6)
- +5 ≡ -1 (mod 6)
- +6 ≡ 0 (mod 6)
- +7 ≡ +1 (mod 6)
- +8 ≡ +2 (mod 6)
- +9 ≡ -3 (mod 6)
- +10 ≡ -2 (mod 6)
- +11 ≡ -1 (mod 6)
- etc.
Monday, October 28, 2019
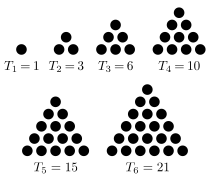
Proving triangular number congruence patterns
1. The formula for triangular numbers is Tn = n(n + 1) ÷ 2
This is common knowledge, but I include it for the benefit of any readers who may be even less mathematically inclined than myself.
The nth triangular number (written Tn) is the sum of the natural numbers from 0 to n. Such numbers are called "triangular" because that number of points can be arranged in a triangular configuration as shown below.
Deriving the formula for triangular numbers is fairly straightforward. Take a given number, n, and write out 1 + 2 + ... + n. The sum of those numbers will be Tn. Now, below that, write the same sum in the opposite direction, n + n-1 + ... + 1. The example below shows what this looks like for n = 5.
Each of the two rows adds up to Tn, so the total of the two rows is 2Tn. If we look at the vertical columns, each of them adds up to n + 1. The first column is 1 + n; the second is 2 + (n - 1); the third is 3 + (n - 2); and so on. There are n columns in all, so 2Tn = n(n + 1). The formula for Tn, therefore, is n(n + 1) ÷ 2.
(Sorry if using an obelus instead of fractional notation makes these equations a little hard to read. It allows me to type them inline instead of inserting an image file for each equation.)
2. For any modulus k, the series of triangular numbers reduced modulo k repeats, with a period no greater than 2k.
This part was discovered by Kevin McCall, though I've reformulated it somewhat.
It is postulated that, for any modulus k, T2k ≡ 0 (mod k). This means that T2k is evenly divisible by k; in other words, that T2k ÷ k is an integer.
Plugging 2k into our triangular number formula, we get T2k = 2k(2k + 1) ÷ 2. Dividing by k gives us T2k ÷ k = 2k(2k + 1) ÷ 2k = 2k + 1. Since k is itself an integer, 2k + 1 is an integer as well. Therefore, T2k ≡ 0 (mod k).
Now consider the next triangular number in the series, T2k + 1. For any given triangular number, Tn , Tn + 1 = Tn + n + 1. (For example, for n = 10, the 10th triangular number is 55, and 55 + 10 + 1 = 66, which is the 11th triangular number.) Since 2k + 1 ≡ 1 (mod k), this amounts (in the modular arithmetic we are using) to adding 1, and T2k + 1 will be congruent to 1 (mod k).
Now the whole series of triangular numbers begins with 0. Then we add 1, then 2, then 3, and so on to infinity to generate the whole series.
- T0 = 0
- T1 = T0 + 1 = 1
- T2 = T1 + 2 = 3
- T3 = T2 + 3 = 6
- T4 = T3 + 4 = 10
- etc.
- T2k ≡ 0 (mod k)
- T2k + 1 = T2k + 2k + 1 ≡ 1 (mod k)
- T2k + 2 = T2k + 1 + 2k + 2 ≡ 1 + 2 ≡ 3 (mod k)
- T2k + 3 = T2k + 2 + 2k + 3 ≡ 3 + 3 ≡ 6 (mod k)
- T2k + 4 = T2k + 3 + 2k + 4 ≡ 6 + 4 ≡ 10 (mod k)
- etc.
We can see that any time Tn ≡ 0 and Tn + 1 ≡ 1 (mod k), the series will repeat. We know that this always happens where n = 2k. Therefore, the period of the repetition must be either 2k or else a number by which 2k is evenly divisible.
3. The period of repetition is always either k (if k is odd) or 2k (if k is even).
If k is and odd number, the series of triangular numbers reduced modulo k will begin to repeat at k rather than 2k because Tk ≡ 0 (mod k), meaning that Tk ÷ k is an integer. Tk ÷ k = k(k + 1) ÷ 2k = (k + 1) ÷ 2. Since k is odd, k + 1 is even, so (k + 1) ÷ 2 is an integer. Tk + 1 will then be equal to Tk + k + 1 ≡ 1 (mod k), and so on.
At this point my direct reliance on Kevin McCall's proof stops. Everything below is my own. (Kevin has proved it all, too, but I have not yet read his proof and will not do so until I have first proved it all myself.)
How do we know that the period is never smaller than k? Might it sometimes be k ÷ 2, for instance? No. While it sometimes happens that Tj ≡ 0 (mod k), where j < k, it is never also true that Tj + 1 ≡ 1 (mod k), which is what is necessary for the series to repeat. Recall that Tn + 1 = Tn + n + 1. Therefore, where Tj ≡ 0 (mod k) and j < k, it follows that Tj + 1 ≡ j + 1 (mod k). The only way j + 1 can be congruent to 1 (mod k) is if j ≡ 0 (mod k), which we have specified that it is not. (With the exception of 0, no number less than k can be congruent to 0 modulo k.)
Therefore, the period of repetition is always precisely k (if k is odd) or 2k (if k is even).
4. The repeating series is always palindromic.
It is postulated that for any modulus k, the series for triangular numbers from T0 to T2k - 1 reduced modulo k (which series goes on to repeat itself forever, as proven above) is palindromic. This means that
- T0 ≡ T2k - 1 (mod k)
- T1 ≡ T2k - 2 (mod k)
- T2 ≡ T2k - 3 (mod k)
- etc.
5. Where k is even, the number at the center of the palindrome is k ÷ 2
Wednesday, October 23, 2019
Triangular number congruence patterns proven
I have only seen his proof of the first of those statements; I am not going to look at the remainder of his proof until after I have proven it myself independently -- at which point I will post both his proof and mine.
Monday, October 21, 2019
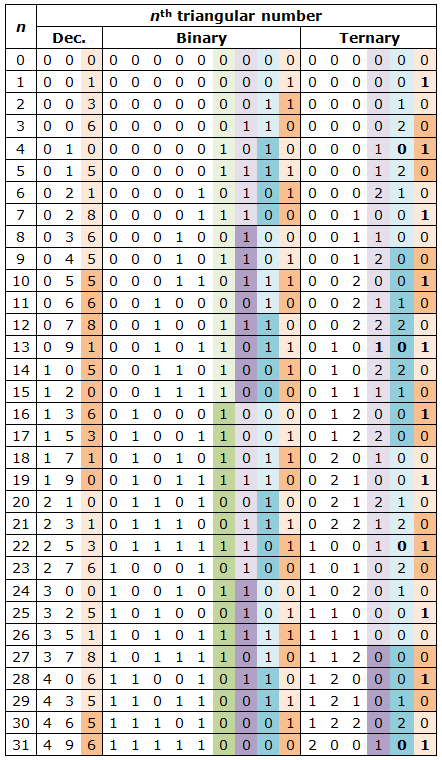
Patterns in the digits of triangular numbers
List the triangular numbers, starting with 0. The final digits of the numbers in the series will exhibit a repeating pattern with a period of 20, and the pattern will be palindromic. The penultimate (tens-place) digits will also exhibit a repeating palindromic pattern, with a period of 200. The repeating palindrome for the hundreds-place digits will have a period of 2000, and so on for any "place" you care to choose.
This is assuming you write the numbers in the familiar decimal system -- but any number base will yield corresponding results. If the triangular numbers are written in base b, the pth-to-last digit will exhibit a repeating palindromic pattern with a period of bp (if b is odd) or 2bp (if b is even).
(Oswald Wirth, whose writings first alerted me to the existence of such patterns, was doing what he called "Theosophic reduction" -- i.e., adding up the digits of a number until a single digit is arrived at. "Theosophically reducing" a number in base b corresponds to taking its final digit in base b - 1.)
The patterns are easiest to see in very small bases such as binary and ternary, shown below with color-coding to highlight the repeating palindromes.
I have still not figured out why these patterns exist. Even stating the pattern algebraically is proving somewhat difficult for someone whose mathematical training is as limited as mine.
Monday, October 14, 2019
Congruence patterns in the series of triangular numbers
By "Theosophic addition," Wirth simply means the operation which yields the series of triangular numbers, where the nth triangular number is the sum of all integers from 0 to n, inclusive; in other words, the nth triangular number is equal to (n² + n) ÷ 2. The first several triangular numbers are: 0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666.
"Theosophic reduction" means adding up all the digits of a number, and then repeating the process as necessary until a one-digit number is arrived at. Mathematically, this amounts to finding the smallest positive integer to which it is congruent modulo 9.
Wirth took the first 21 triangular numbers (beginning with 1) and "Theosophically reduced" them, yielding this series: 1, 3, 6, 1, 6, 3, 1, 9, 9, 1, 3, 6, 1, 6, 3, 1, 9, 9, 1, 3, 6. As you can see, the same series of 9 numbers (1, 3, 6, 1, 6, 3, 1, 9, 9) repeats itself; and if you keep going beyond 21 (which is where Wirth stopped because he was considering the numerology of the 21 Tarot trumps), it becomes apparent that it keeps repeating itself forever.
Wirth took this pattern as confirmation of the traditional (ultimately Pythagorean) numerological idea that the first 9 natural numbers are the building blocks of all the rest, and that that "the decad is a new monad." However, it seemed pretty obvious to me that there is nothing special about the number 9, and that the 9-based pattern Wirth found was almost certainly an artifact of the use of the decimal system in the "Theosophical reduction" -- such that "reduction" meant finding congruence modulo 9 -- and that other moduli would yield other patterns.
I also saw that Wirth had missed an interesting pattern in his integer series because he had started with 1 rather than 0, and because he was thinking in terms of "reduction" rather than congruence. (Nine is congruent to 0 modulo 9, but you can't arrive at that 0 by adding up digits in the "Theosophic" fashion.) If we start with the 0th triangular number (which is 0), and if we "reduce" multiples of 9 to 0 rather than to 9, the repeating series becomes (0, 1, 3, 6, 1, 6, 3, 1, 0) -- which is a palindrome!
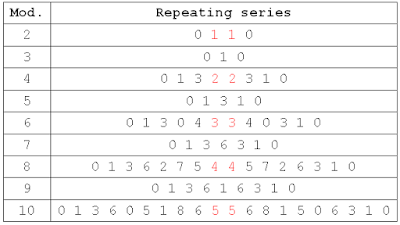
I decided to check other moduli, starting with the easiest, which is 10. Any decimal number is congruent modulo 10 to its final digit, so look back at that list of triangular numbers and look at the final digits. The first thing you will notice is that certain final digits (2, 4, 7, 9) never occur at all. Look a little further, and you will see that there is a repeating pattern. It has a period of 20 (not 10, as we might have expected) -- and, sure enough, it is a palindrome: (0, 1, 3, 6, 0, 5, 1, 8, 6, 5, 5, 6, 8, 1, 5, 0, 6, 3, 1, 0).
It is natural to jump from this to the induction that every modulus will yield a palindromic repeating pattern, and this turns out to be true for all the moduli I have looked at, as the table below shows. I have used centered alignment to highlight the palindromic nature of the repeating series.
From this sample, it appears that:
- Any modulus, m, yields a repeating palindromic series of congruences for the series of triangular numbers.
- If m is odd, the period of the repeating series is equal to m.
- If m is even, the period is equal to 2m, and each of the two numbers at the center of the palindrome is equal to m/2.
Ace of Hearts
On the A page of Animalia , an Ace of Hearts is near a picture of a running man whom I interpreted as a reference to Arnold Schwarzenegger....
-
Following up on the idea that the pecked are no longer alone in their bodies , reader Ben Pratt has brought to my attention these remarks by...
-
1. The traditional Marseille layout Tarot de Marseille decks stick very closely to the following layout for the Bateleur's table. Based ...
-
Disclaimer: My terms are borrowed (by way of Terry Boardman and Bruce Charlton) from Rudolf Steiner, but I cannot claim to be using them in ...